One benefit of the Nomothetic Theorem is that it is not necessary to understand how everything works and how everything is related in order to be able to predict what will happen next. In fact, the theory tells us that there are certain situations where it is not possible to define position or events except within a range. The Theory of Volatility tells us that it is fruitless to try to measure, or predict, any position within the normal range of volatility. By definition, the range of normal volatility defines an area in which any position is subject to random change. One of the realities of life is that you cannot always know exactly what is, or what will be.
The Nomothetic Theorem helps us to look at dynamic complex systems within a framework of probability. It defines areas in which we cannot have any certainty, or even any reliable probability of an event occurring. However, the Theory of Stability also tells us that complex systems tend to net out imbalances and settle on a trending norm. We can not only attempt to identify that norm, but we can also attempt to understand deviations from the norm. It is this definition of a norm and deviations from the norm that allows us to make certain predictions.
Some specific examples will help greatly. Let us relate the Nomothetic Theorem to market pricing. It seems logical that the Nomothetic Theorem should have a lot to say about the way stock prices move.
The Nomothetic Theorem does not provide a fundamental explanation of why things are happening in each particular case. That is to say, we may not be aware of the specific motivation for an individual event. However, through the dynamics of complex systems, the Theorem focuses on the net result of all forces on a system and thus reveals and predicts the kinds of things that we can expect to see happen. You have heard the expression "Actions speak louder than words". That is the case here. For example, if we observe the repetitive event of geese consistently flying south, we are encouraged to make some predictions about more geese flying south. Eventually, a pattern may emerge regarding the migratory habits of geese. (Specifically, geese tend to flock south with the onset of winter. Additionally, they do not travel randomly as individuals. When it is time to move, a wholesale migration develops.) Once we identify the pattern, we can search for reasons to explain the pattern. Although understanding why things happen is useful, knowing what is going to happen (regardless of whether we understand why) is more important for survival. Predicting an event by knowing the end result of a motivating force is more important initially than understanding the force itself. Since force is invisible, we can easily be led astray by making suppositions about the motivating cause of events. But action is reality. Physical events do not lie. Whether action is the result of one force, or the net result of many forces is less important initially than being able to predict the final outcome.
Another way of expressing this concept is to say that all relevant information is contained in the net result. If a force exists, its effect will be revealed in action (including the special case of lack of action). If a force does not exist, its lack of effect will be revealed in a different net result. If two opposing forces perfectly cancel each other out, then for the specific event in question, it is not necessarily more useful to know they both exist than to believe that no force exists. There are perhaps many reasons for geese to fly south, none of which may be sufficient to allow accurate prediction. The complex interaction of the length of day, temperature, food supply, weather, habits of predators -- all of which may signal the approach of winter -- creates a complexity that is difficult, if not impossible, to deal with. But when you actually see a goose fly south, you know something concrete. Once the first goose flies, it is possible to predict that more will soon follow.
One particularly illustrative area in which the Nomothetic Theorem can be usefully applied concerns free-market pricing. There probably is no such thing as a market totally untainted by government regulation, tax codes, moral prohibitions, internal inequities, and other constraints. But, for the sake of example, let us for the moment talk as if we had totally free markets. Later on we can consider what happens when additional forces are applied to any complex system, including an economic system.
The question of value is at the heart of any transaction between a buyer and seller. The price of a product or service derives from a consensus of its value. Just as "beauty is in the eye of the beholder", anyone can pay any amount for anything, and thus prices can fluctuate wildly from one transaction to another. But price stability, or at least effective price discovery, is a key ingredient of an efficient market. Widespread communication leading to an informed consensus of value is the key to price discovery. In a free-market economy, price discovery is an example of the Theory of Stability. Price discovery is a process that causes an economic system to evolve toward an increasing level of stability. For a framework of stable pricing to develop, we depend on the assumption that supply will eventually come into balance with demand, and agreement will develop regarding the relative value of one object or service compared to another. Prices may wander considerably while the market seeks information and while buyers and sellers try to find each other and develop a common structure within which to transact business. But the Theory of Stability tells us that eventually a price level should be reached that remains fairly stable within a normal range of volatility.
Arbitrage is one way in which markets find stability. As a simple example, suppose gold sells in New York for $290 per ounce and in London for $300 per ounce. Let us assume it costs $2 to insure and ship one ounce of gold across the Atlantic. There exists an incentive for someone to buy gold in New York for $290 and sell it in London for $300. A ten dollar difference minus a two dollar expense returns eight dollars in profit, or a two and three quarter percent return on an investment of two hundred ninety dollars. If it takes one week to complete the transaction, including shipping and receiving the gold, this could be done fifty-two times a year for a 143% annual profit! Obviously, if enough people engaged in this arbitrage, the supply and demand for gold in both London and New York would change and the price difference would narrow. Once the price is quoted at $295 in new York and $296 in London, there would be no further advantage to arbitrage. The price of gold would presumably remain stable (in a narrow range of volatility) until some other event caused a shift in supply and demand.
Another familiar mechanism of free-market economies that leads to price discovery and stability is competition. Imagine that there are five different grocery stores selling a two liter bottle of Coke, all for different prices as follows:
| Store A | $0.99 |
| Store B | $1.09 |
| Store C | $1.19 |
| Store D | $1.29 |
| Store E | $1.39 |
We can assume that there are situations where people will pay a premium for a product due to convenience, location, service, or some other factor. But a 40% spread in price is usually too much of a difference. In this case, people will tend not to buy from stores D & E and business will flow to store A. To stay in business, stores D & E may have to lower their prices. The price of Coke may narrow to a range between $0.99 and $1.19 and we might identify the norm as $1.09. But store A may discover that it can't make money selling Coke at $0.99. Or store A may figure out that it can make more money by selling Coke at $1.09, because even at the higher price its volume of customers does not diminish and it has a larger profit margin. So store A may raise its price and a new price range and norm may be established. Regardless of how it works out, competition promotes price discovery (in relation to value) and should eventually narrow the range of price differences.
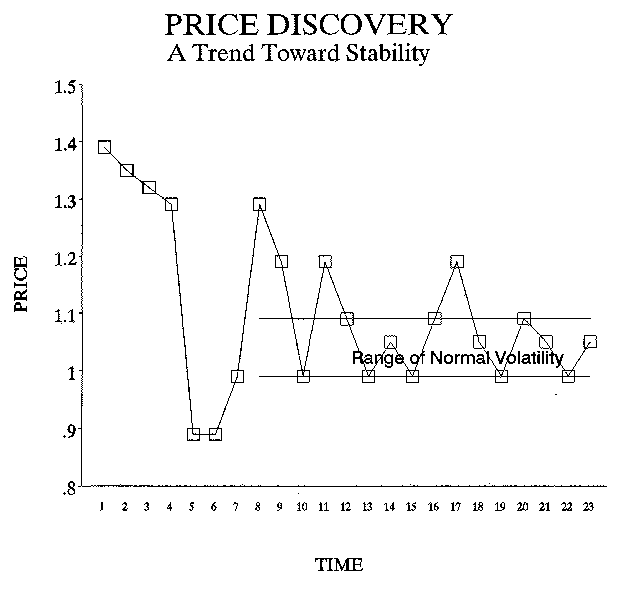 |
There is yet another similar situation where the same forces are applied across time. Suppose there is only one store in town that sells Coke. It tries selling it at $1.39 and finds some people buy it, but not many. It reduces the price to $1.19 and finds it can do a good business but it is still not selling the volume it expected and it needs to clear some inventory. It has a sale at $0.99 per two liter bottle and its shelves are cleaned out. It now starts experimenting with the price of Coke, sometimes pricing it way down and using it as a loss leader to bring in customers, and other times pricing it up to take advantage of demand during holidays and hot summer months. The smart consumer waits and watches, stocking up during the periods of low prices, and avoiding purchasing during periods of high prices. The actions of the consumers will tend to force the store toward more stable and reasonable prices while other events will always maintain some volatility in the pricing.
As we know, volatility means a lack of predictability. If we can't predict accurately, we can't plan dependably. Without dependable plans, we have to rely on contingencies and alternatives, or we have to accept a certain level of failure. All of this means added cost. Since high volatility means high transaction risk and high cost, it is for the public good that most governments try to promote efficient and stable markets. The more efficient a market is, the more quickly an appropriate price level is found. Because it is in the best interest of trade and commerce to have efficient markets, various regulated centralized public markets are established in most countries. Examples are food markets, commodity markets, labor markets, and stock (capital) markets. One example of a public market in the United States is the New York Stock Exchange. The stock exchange is a centralized market. It makes it easy for buyers and sellers to find each other because the New York Exchange is in one specific geographic location. It is also an auction market which allows the price level to be set by the best bid and the best offer.
With today's worldwide dissemination of electronic quotes, stock markets are usually very efficient. Additionally, improvements in technology now means that markets can be efficient without having to be geographically centralized. An example of a decentralized market is the NASDAQ (National Association of Securities Dealers Automatic Quotation System) over-the-counter market. Although geographically decentralized, the NASDAQ market makers are linked together by an electronic quote system that allows centralized communications and price comparisons. (The world wide web is doing the same thing with other markets and with society in general.) With modern efficient markets, we would expect volatility to be quite small. However, the introduction of technology to improve the efficiency of markets brings with it a shift in the cause of volatility. Volatility which used to be caused by inefficient markets due to a shortage of information (or a long lag time for the widespread dissemination of information) is being replaced by volatility from an increasing supply of changing information which is widely and quickly disseminated along with prices. The constant flow of new information causes a continual readjustment of perception of value, and therefore price. Price changes in an efficient market are tolerated as being appropriate. However, price changes are considered inappropriate and undesirable in a inefficient market (a market that allows manipulation or unequal access to information or unreliable information). Because inefficient markets are considered morally unfair as well as economically costly, many regulations are designed to prohibit trading that will exacerbate volatility or provide an advantage that unfairly distorts equality in the market place. The danger of such regulations is that they may do more harm than good. Some volatility is necessary to promote price discovery. And some volatility is necessary to create trading opportunities. Without sufficient trading (which reflects competing opinions of value), markets lose their liquidity and become inefficient. Therefore, the most efficient dynamic markets are those that combine elements of both stability and volatility.
Applying the Theory of Volatility to understand free-market pricing is not only useful to merchants and consumers, but is also particularly useful for investors because of the unique structure of our modern markets. Today's markets are not only efficient and liquid, they also contain many derivative instruments that allow investment in the price movement of synthetic concepts, such as indexes (groups of securities), and investment in events, such as strike prices and redemption values. Investing in price "events" offers tremendous flexibility as opposed to only being able to invest in physical commodities or commercial enterprises. (A derivative instrument is a security that derives its value from another security. For example, an option is a derivative instrument that obtains value from the underlying security that can be purchased with the option. Unfortunately, some derivatives are so complex or are being used in such complex strategies that hundreds of millions of dollars have been "accidentally" lost by professional traders that say they didn't fully understand the risk of their strategy. This has given derivatives a bad name in some circles. But this is just a typical case of blaming the vehicle instead of blaming the driver.) With all of today's derivative instruments, it is now possible and equally easy to trade for a profit in rising markets, falling markets, or flat and unchanging markets. The only challenge for the investor is to correctly identify the next market move and position correctly to take advantage of it.
 |
Investors seek to make money from changes in price. As we know, prices fluctuate constantly within a normal range of volatility. The Theory of Volatility tells us that predicting the next price change within the normal range of volatility is not possible. It still may be possible to make a profit from small random fluctuations by using arbitrage techniques, but in a highly efficient market place this is not a feasible strategy for most nonprofessional investors. As a general rule, investors seek to make money from system drift -- the trend, or general change in prices over time (i.e. the stock buyer hopes the price of his stock will trend up over time regardless of intermediate volatility). Investors would also like to make a profit from "events" that can cause a sudden shift in prices and often a change in trend. Unfortunately, unless you are privy to inside information or good at fortune telling, it is hard if not impossible to correctly predict market moving events.
It would seem that the investor's opportunity to make a profit is quite limited. As a result, many people believe that a "buy and hold" strategy designed to take advantage of the long term uptrend in the stock market is the only reasonable strategy for the prudent man to adopt. This strategy is endorsed by many very high profile and successful investors such as Peter Lynch, former portfolio manager of the Fidelity Magellan Fund, and Warren Buffet, an extremely successful Graham & Dodd "value" investor. But the "buy and hold" strategy is not the only strategy that works. In fact it has some serious shortcomings. The "buy and hold" method does not work in flat or down markets.
The individual investor has a unique advantage that is rarely understood and appreciated by the non-professional. The individual investor has the luxury of being able to pick when to invest and how much to commit to any position. This may not seem like much of an advantage. But compare this freedom to the requirements placed upon a specialist working on a stock exchange or an Over-The-Counter market maker. These people have to be willing to step into the market any time it is necessary to provide a liquid and orderly market. They may have to take positions they don't really want at times they don't want. (This is similar to a merchant having to stock a broad inventory of articles "just in case" someone might want a particular item, when in reality most of the inventory is stagnant and nonproductive.) Many other institutional investors have similar constraints and demands that limit their investment freedom. Imagine trying to manipulate a $20 billion investment portfolio in a rapidly moving market without adding to the price volatility. But if you are an unfettered individual investor, you have complete freedom to "cherry pick" the markets. The question is, how can you employ this advantage to increase profitability?
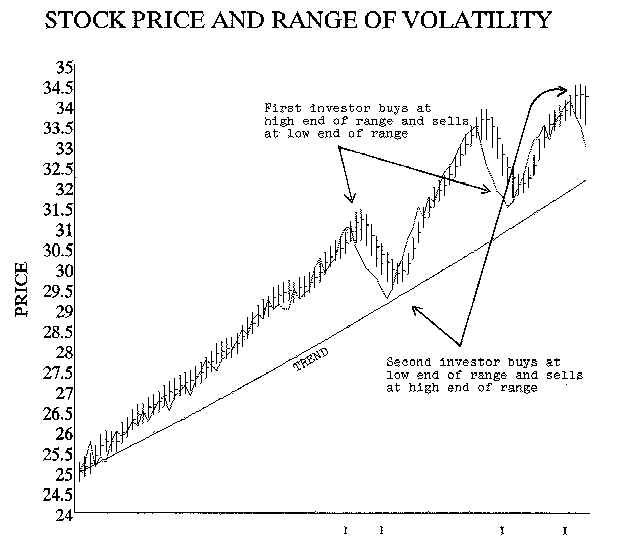
There are actually several trading techniques that can be used very effectively. One is a very simple application of the Theory of Volatility. It is true that the theory says we cannot not know the direction or degree of the next market move when we are in the normal range of volatility. But the obverse is also true. We can be confident that prices will oscillate within a definable range. There is every reason for the astute investor to use this volatility to his advantage when investing with a trend.
Compare two investors who have been watching a stock move up, and each believes the stock will continue to move up at least another ten percent. They both want to own the stock and hold it for the system drift, or upward trend, that they perceive will continue. One investor understands the Theory of Volatility and the other does not. In our example, both investors are correct, and over a period of two months the stock price does increase an average of ten percent. However, after owning the same stock for the same length of time during approximately the same period, one investor only made three percent and the other made 15%. The difference in performance resulted from the effect of the normal range of volatility surrounding this stock price.
The first investor watched the stock price progress through $28.50 and $29, then $30, and $31. He had no real concept of the consensus value for the stock. He just knew it was going up and, for various reasons, including momentum, he felt the trend would continue. When the stock hit $31, he decided "no time like the present" and he bought it. He watched with dismay as the stock dropped below $30 and oscillated in the high twenties. He was relieved and felt vindicated when the stock climbed back above his purchase price and progressed through $32 and $33 up to a high of $33.50. But when it then dropped to $31.75, he panicked and thought maybe the trend was over. He was relieved to be able to get out with a profit when it ticked up to $32. This investor did not understand normal volatility and could not differentiate between volatility and the price trend of the stock.
 |
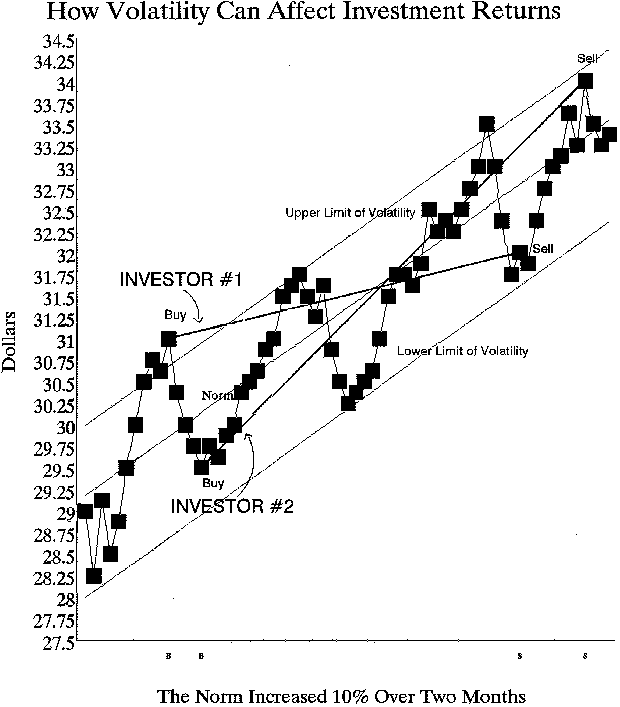 |
The second investor saw the same stock also progress through $28.50 and $29, then $30, and $31. He also believed the stock would continue up. But he understood volatility and concluded that the consensus value for the stock was $30. At $31 the price was at the high end of its normal range of volatility. Therefore he waited until the price dropped below $30. He was able to buy it a few days later at $29.50. Our second investor also watched the stock move up and peak at $33.50. He was tempted to sell there because it was in the upper range of normal volatility, but he decided to stick with the trend. When the stock dropped below $32 he did not panic because, although it was displaying some weakness, the price was still in an uptrend. A few days later when it hit $34 at the upper limit of volatility, he took his profit.
The chart shows that the norm moved from $30 to $33 which is a ten percent increase. One investor took advantage of volatility to realize a 15% gain. The other investor was confused by the same volatility and only realized a 3% gain.
Another way of visually understanding this is to just focus on the deviation from the norm as in the chart below. The first investor ignored random volatility and purchased above the norm and sold below the norm. The second investor used normal volatility to make his purchase below the norm and sell above the norm.
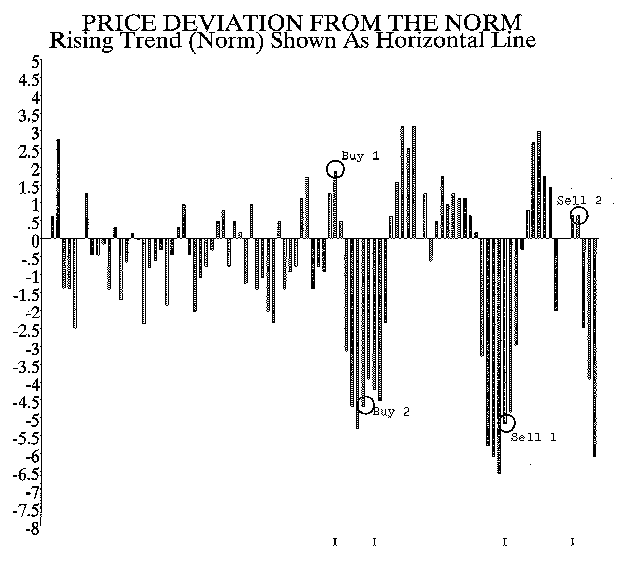 |
Investor 1 bought high and sold low on a relative basis. Investor 2 did better.
Most people do not see any advantage to volatility. When computerized trading started to move the stock markets in the 1980's, nervous investors and regulators began to question the wisdom of allowing baskets of stocks to be bought and sold automatically by computer. One of the results of the market crash in 1987 and the scare that it gave to regulators was the restriction, under certain conditions, of large buy and sell programs. There is a strong desire among many people to increase the amount of regulation designed to damp down market volatility. However, it can be argued that volatility is necessary and appropriate to provide trading opportunities and thus liquidity and market efficiency. It is more likely that people who want insulation from volatility really just want insulation from loss. They want the government to protect them from loss as if they have some natural inalienable right to profit. The problem is perhaps not with the markets, but with the typical investor's inability to deal with complexity. The average investor is perhaps confused by market volatility because he does not have the tools to analyze complex systems and does not understand the dynamics of valuation.
Coping with volatility involves thought and work. Determining value requires research, and certainly holds the possibility of mistaken judgement. Investors that are used to purchasing bank certificates of deposit with guarantees attached are unfamiliar with the concept of having to put forth work and assume risk in order to expect a greater profit. The typical investor would like to buy a mutual fund and see his money grow at 50% per year every year. Wouldn't we all! But markets don't skyrocket in one direction without risk. People naively think they can make a greater profit investing in a mutual fund without doing any work than they can make by owning a business or owning real estate and putting up with the headaches of being a manager or a landlord. It is interesting to note that nobody complains about volatility when the stock market is going up. But people come out of the woodwork screaming when it suddenly goes down. That simply demonstrates the large number of investors who want to "buy and hold" because they naively believe that stock markets should always go up, compared to (the fewer in number but probably more sophisticated) investors who trade based on the dynamics of a complex system, and may at times sell short. (Short selling allows a profit to be made in a declining market.)
But enough of this editorializing. Let me tell you about another, perhaps more interesting trading strategy that develops from the Nomothetic Theorem. The key to successful investing is simply being able to make reliable predictions. Obviously, the number one rule of investing is: DO NOT LOSE MONEY. This means: you do not invest when you don't know what is going to happen. If most people abided by this maxim, they would probably never invest. The "buy and hold" strategy addresses this dilemma by claiming that we cannot know what will happen in the short term or intermediate term. All we know for sure is that the longest trend we have been able to observe so far, essentially the entire history of our modern markets, tells us that eventually the market goes up and if we are patient enough we should realize a profit. However, that same history will demonstrate that there have been many individual investments that have never gone up and, even with a broadly diversified portfolio, there have been whole decades when an investor would not have made a profit in the stock market (especially in inflation adjusted terms). Therefore, although the buy and hold strategy has worked well from 1982 through the 1990's, there is certainly no assurance that it will continue to work over any particular period of time in the future. It would be a lot more efficient if we could just invest during the periods when we knew we would make money and not invest (or, invest somewhere else where the opportunities are more favorable) during the periods when we would lose money. But we have to be able to reliably predict the future movement of prices in order to do this. The usefulness of the Nomothetic Theorem is its ability to help us differentiate between things we can predict with a reasonable degree of reliability versus things we can't.
Understanding the role of volatility and using it to the investor's advantage is just one small example of how the Nomothetic Theorem can be used constructively to improve investment returns. There are some much more powerful applications of the theory that depend on its predictive abilities, but they are not being placed in the public domain at this time. To learn more about investment applications, follow the link below.