When one thinks in terms of the Nomothetic Theorem, common events are seen in a new context. Something as simple as watching steam float up from a hot cup of coffee on a cold day is a good visual for the theorem's explanation of complex systems.
Brownian motion was briefly mentioned under the discussion of symmetry. Most people learn about Brownian motion in high school as the explanation for why molecules of steam or particles of smoke float about randomly. Specifically, in 1827, the biologist Robert Brown observed under his microscope that tiny pollen grains suspended in water moved about, even though the water appeared to be perfectly still. The logical explanation for this movement was the atomic theory. If matter is not continuous, but in fact made up of tiny particles called atoms and molecules, then the motion of the tiny particles jostling into each other could explain Brownian motion.
Think about the Theory of Volatility. All complex systems experience continuous random motion. This pervasive volatility is found at the atomic and sub-atomic level. Now picture a cloud of vapor, or if you prefer, a cloud of smoke, placed in the corner of a large closed box. The Theory of Volatility tells us that the cloud will not stay still. The Theory of Stability tells us that the complex system of particles will evolve toward increasing stability. So the Nomothetic Theorem presents a tug of war between the natural volatility of the particles in the cloud and the desire for the system to be stable. How is this conflict resolved? Understanding the answer to this question allows us to predict what will happen to the cloud.
Of course you know the answer from experience. In spite of the random chaos of Brownian motion, the system has a trending norm. We know from observation that the cloud wants to spread out. The particles want to disperse. The system will trend toward a position of equal distribution. The cloud will eventually become evenly distributed throughout all the space available to it. Once this happens, the motion of the atoms or molecules will continue randomly in a norml range of volatility, but the system will be stable.
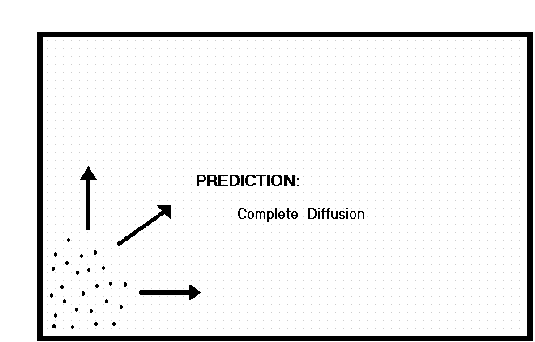 |
This is a simple explanation of the Nomothetic Theorem. What Robert Brown observed was an example of the Theory of Volatility. The motion inherent in a complex system of atoms and molecules must resolve itself in the direction of increasing entropy. Thus the Theory of Stability allows us to predict that the cloud will not remain sitting in one corner of the box. It must disperse itself evenly throughout the box.
This line of reasoning is a step removed from the linear cause-and-effect process that most people tend to think of. It isn't feasible to take the energy of an individual atom and mathematically compute how it will affect all the other particles in the system, but that doesn't prevent us from making accurate predictions about the entire system, regardless of its complexity.
STABILITY & ENTROPY
While explaining Brownian motion above, I said we know from observation that the cloud wants to spread out. The particles want to disperse. The system will trend toward a position of equal distribution. The cloud will eventually become evenly distributed throughout all the space available to it.
Well, it may be true that we observe that, but how do we know that this is the way it has to be? Why does the Theory of Stability predict that this is what will happen?
Let me see if I can explain that part a little better. Since this is an example taken from physics, let me describe the Theory of Stability in the language of physics.
Potential is a measure of the ability to perform work. Work is defined as a force applied across a distance. Thus, a one pound weight raised one foot above the earth has a potential of one foot pound. Potential is the entrapment of energy that can perform work. The concept of potential can be understood by the fact that the energy that was spent to raise the weight up one foot can be released and perform work when the weight is allowed to drop back toward earth. This energy might be used to run a clock, raise another weight, or hammer a nail. If the weight is simply allowed to drop, the energy is dispersed in the form of noise, heat, and perhaps the dislocation of other matter that is hit. (The law of conservation of energy says the energy must be accounted for somewhere.)
The important feature of potential is the degree of equality or inequality of forces. Since there is an unequal balance of forces when potential energy is released, the force travels across a distance and work is performed. If there is no opportunity for inequality, there is no release of potential to perform work. A crude example of no potential is a cork floating on a smooth body of water. The force of gravity is equally offset by the force of buoyancy. (Although it can be argued that there is potential in the system i.e. the cork may eventually get waterlogged and sink, there is no immediate inequality to allow the potential to perform work.) It requires the introduction of new energy to move the cork in any direction. It would take additional energy to raise the cork up above the water, and it would take additional energy to push the cork down below water. There is no mechanical energy contained in the cork when it is floating in balance. (Of course energy can be released by burning the cork or removing the water, but that is outside of the point I wish to make.)
One is stimulated to think about the Theory of Stability in the situation where a single application of outside energy is applied in a way that causes the cork to bob up and down in the water. The Theory of Stability predicts that the interaction of the cork and the water and the air will evolve into a stable relationship. While a regular oscillation is a form of stability, there are considerations of pressure and friction to contend with in this example. These transformations of energy interfere with a continuing regular oscillation. Observation over time shows that the cork stops bobbing and eventually floats quietly. The reason this happens is because energy is lost from the system. When the cork bobs up and down it displaces air and water. One can actually see pressure waves of water circle out from the cork. The waves are a visual pattern of energy being carried away from the cork. (The energy is dissipated as it performs work. The waves show us force being applied across a distance.) As energy dissipates, the cork moves less and less. This is an example of entropy.
I used to think that a perpetual motion engine was a fascinating idea. But a little reflection reveals that if an engine is going to perform any work (even if it is just the work of overcoming friction to keep running), it will release energy. That energy needs to be replaced in the form of fuel for the engine. Fuel is just another word for potential. But the creation of potential requires energy. If an engine is going to run perpetually, it needs a source of infinite potential. Even if there were an infinite amount of energy in the universe that could be harnessed, if the energy was in a state of maximum entropy, it would be useless. It takes energy to harness energy to create potential. Here is where the discussion gets interesting. Random energy (disorganized energy, dispersed energy) is not very useful. Random energy is or becomes diffused energy which loses its level of inequality. (Remember, energy seeks to cure an imbalance.) Without inequality, energy loses its character as energy because it no longer has the potential to perform work.
The tendency of energy to dissipate and diffuse means that entropy and the Theory of Stability are inextricably tied together. You have perhaps heard the expression that, "When you reach the top, there is no place to go but down". This is true in a larger sense than just a description of social relations. A position of high potential is a position of instability. A position of decreasing potential (increasing entropy) is a position of increasing stability.
Going back to the previous example of Brownian motion (where a cloud of particles is in one corner of a box) we have a situation of inequality where the energy potential of the particles are massed in one corner of the box, while the other areas of the box are empty. Energy always seeks to cure an imbalance. The imbalance is removed and the state of maximum entropy and greatest stability is reached when all the particles are evenly distributed throughout the box. The system of particles must move to this state of greater stability, and it cannot be reversed without the introduction of additional (new) energy.
This tug of war between volatility and stability is simply a useful way of understanding complex systems. I am not trying to tell you that things work any differently than you have always observed them to be. I am trying to give you a framework within which to place your observations and be able to connect them in a coherent manner. If you can understand complex systems as being nonlinear, but then deal with them in the linear directional context of time, you have some hope of successful prediction.