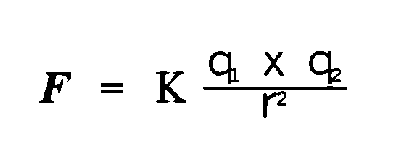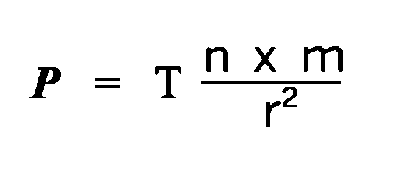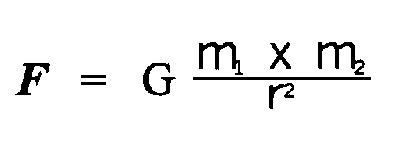ANECDOTAL SUPPORT
There are many interesting applications of the Nomothetic Theorem. But before we
discuss some of the ways to apply the theory, let's consider how the theory relates to the existing
body of commonly accepted knowledge. I have already talked about Newton's first law of motion
that describes the state of stability (uniform motion) that is the natural state of all objects unless
acted upon by a force. This is also the state of stability that all objects seek to return to after they
are subject to an outside force Complex systems are no different than an isolated object. As soon
as all outside forces are removed from a system, the internal forces go through a period of
redistribution, seeking equilibrium, which ultimately causes the system to evolve toward a natural
state of stability similar to that which Newton describes for single objects. (Remember, simple
objects of the kind Newton thought about are actually complex systems of atoms and molecules.)
The second law of thermodynamics provides a more direct example of the Theory of
Stability at work in complex systems. As you recall, the Theory of Stability was derived from the
statement that energy seeks to cure an imbalance as it moves in the direction of increasing
entropy. The second law of thermodynamics tells us that temperature differentials will tend to
diffuse and neutralize until a state of maximum equilibrium is attained for a system. The law says,
in an isolated system, entropy cannot decrease. Therefore, the degree of equilibrium increases as
entropy increases and the state of greatest equilibrium corresponds to the state of greatest
entropy. In other words, the second law says equilibrium is the preferred or most stable state of a
thermodynamic system.
Because most complex systems are dynamic for a period of time, even after they are
isolated, the Nomothetic Theorem is interested not just in the end result, but in the process. That
is to say, it is useful not only to know what equilibrium point a system is evolving toward, but also
why, and how it is going to get there.
Another example of the Theory of Stability can be found in Pascal's Law. Blaise Pascal
was a French mathematician who arrived at the following conclusion in 1647. The pressure
applied to an enclosed fluid is transmitted equally in all directions. And the force exerted on any
particle within the fluid is the same in all directions. (If the forces were unequal, the particle
would move in the direction of the net force until all forces come into balance.) From this we can
see that the pressure exerted against the interior walls of any vessel is always equal, and
perpendicular to the wall at every point. This is exactly the same conclusion you would arrive at
with the Nomothetic Theorem, only stated slightly differently. The Nomothetic Theorem would
say all forces in a complex fluid system will eventually net out to a maximum level of stability.
The Nomothetic Theorem is in harmony with Pascal's Law but also looks at the dynamics of the
system. Pascal's law recognizes that a system will evolve to equilibrium and focuses on that final
point of equilibrium. The Nomothetic Theorem focuses on the process of moving toward stability
over the period of time that it takes for forces to reach equilibrium. If you fill a balloon with
water (ignoring the effects of gravity and assuming the balloon is constructed evenly), we expect
to see a round balloon. This would be the normal position of stability for the fluid system as
predicted by Pascal's Law. Now if you introduce a one-time mechanical force by hitting the
balloon, we see the balloon distend and oscillate as the water sloshes back and forth, stretching
the balloon. Although the oscillations may initially be erratic, the Nomothetic Theorem predicts
that the system will stabilize. If the balloon were perfectly elastic and there were no friction or
other forces, stability might mean continual regular oscillations. When we take friction into
account, stability means returning to an original static round shape. But regardless of the
conditions, as long as no new outside force is applied, the system will stabilize.
Another bit of anecdotal support for the Theory of Stability comes from the British
chemist Joseph Priestley who, in 1766, demonstrated that an electric charge will distribute itself
uniformly over the surface of a hollow metal sphere and no charge and no electric field of force
exists within such sphere. This is a further example of forces coming into balance, and of
entropy(1).
Until the early part of the twentieth century, one of the basic principles that we have come
to accept as a result of empirical observation is the concept known as the conservation of energy.
This principle states that energy can only be transformed. Energy cannot be created or destroyed.
A similar principle of conservation of matter was also believed to be true. But in 1905 Albert
Einstein demonstrated the conversion of mass to energy with his now famous formula E = MC2 (E
= energy, M = mass, C = speed of light). The convertibility of mass and energy means the two
original concepts are now unified into one principle of conservation of mass and energy. The only
thing that makes a solitary, closed, complex system interesting is the distribution of mass and
energy within the system and the process of evolution toward stability. The Theory of Stability
predicts that our entire universe is evolving toward an ultimate state of stability. However, the
end result is less interesting than the process. And the Theory of Volatility explains a lot of the
dynamics of the process.
In 1827 a British botanist named Robert Brown discovered a physical property that is
called Brownian motion. Robert Brown observed that particles suspended in a fluid are kept in
constant motion. It was theorized that particles suspended in a fluid are struck at random due to
the constant inherent motion of the molecules of the fluid. There is an observed relationship
between motion and heat, because increased temperature produces increased activity. This is a
physical example of the Theory of Volatility ("All complex systems experience continuous random
motion"). With regard to molecules, the Theory of Volatility is supported by the Kinetic Theory.
The Kinetic Theory says that molecules are in constant motion, reaching a state of rest only at the
temperature of absolute zero. (A molecule is the smallest unit of matter, either one or a group of
atoms, that retains the properties of the matter in question.) Molecules are made up of atoms.
The Atomic Theory also refers to the constant random motion of atoms and the particles that
atoms are composed of. Thus, even at the molecular, atomic, and subatomic level, the Theory of
Volatility and the Theory of Stability apply.
In 1901 the German physicist Max Karl Ernst Ludwig Planck proposed a universal
constant of nature, known as the Planck constant. Planck concluded that light waves were
actually emitted in discreet units called quanta. The energy of each quantum is the frequency of
the light, or radiation, multiplied by the universal constant. This was the beginning of the
quantum theory and the aggregate study known as quantum mechanics. In 1926, another German
by the name of Werner Heisenberg formulated his uncertainty principle. The uncertainty principle
concluded that in order to measure the position of a particle in space, you need to use at least one
quantum of light. The energy of the quantum will disturb the particle and thus introduce
uncertainty into the measurement. In fact, the more accurate the measurement, the shorter the
wavelength of light required, and the higher the energy of a single quantum, thus disturbing the
particle by a greater amount. In other words, we have to live with uncertainty because the more
accurately we try to measure a position, the more our act of measuring will disturb the results.
The Theory of Volatility takes this concept a step farther by saying that it is fruitless to try to
measure any more accurately than up to a range of normal volatility, because within that range
any position measured more accurately is subject to random change.
Quantum mechanics progressed with the contributions of Niels Bohr and the American
scientist Richard Feynman to the conclusion that electrons do not act entirely like particles and
follow a single path in space-time. Instead, electrons travel by every possible path from one point
to another, more like a wave than a particle. But this then places the electron in a range or area of
space-time, not at a specific point. So where the Theory of Volatility states that all complex
systems experience continuous random volatility, we can see some basis in physics to support the
fact that volatility or uncertainty exists at a very fundamental level in the subatomic physical
systems of our universe.
1. The electric charge is distributed evenly over the surface of the metal sphere because the charge is carried by
particles called electrons which are evenly distributed. Why aren't the electrons distributed evenly throughout the
sphere like gas inside a balloon? The answer is that gas distributes itself due to the inertia of mechanical force
from the gas molecules bumping into each other, but electric force can act across a distance through a force field.
Electrons will tolerate being close to a few neighbors on the surface of the metal sphere in order to be as far away
from the majority of the other electrons across the sphere. The effect of achieving an equilibrium of forces, and
thus a state of stability, is the same.
Where does the Nomothetic Theroem come from? Is it something made up or
something discovered?
The answer is neither, or maybe both. Anyone can go out and gather information. If you
live for five hundred years, you can gather a lot of information. Is that what we call discovery? I
don't think so.
The act of discovery involves finding something new, something previously unknown.
That is different than just gathering together known things. But sometimes just rearranging or
connecting known things leads us to something new. A new use for a known thing is a discovery.
With regard to information, there is a significant step between gathering facts, and then
converting the raw data into something useful. Knowledge isn't just a collection of data. Useful
knowledge is the conclusion that can be drawn from the data, the recognition of a pattern or
causality, the building of a template that can be reused. The combination or assembly of
information, with the use of logic, into a meaningful structure is what makes information useful.
If I take an existing piece of music and rearrange the instrumentation, have I created a new
song? Of course not. I have simply created a new arrangement. But let us extend the logic of
that argument. All seven notes of the scale with their corresponding sharps and flats are known
by every western musician. Therefore any song I write is simply a rearrangement of those seven
notes. At what point does a rearrangement become a new song? Or at what point is a new song
simply a new arrangement?"
Questions of boundary are difficult to answer. And some questions may not be worth
answering. Where does the boundary of one song end and the boundary of another song begin?
It is like looking at a rainbow and asking where does one color end and the next color begin.
Interesting things happen at the boundaries of systems, and that is one of the important areas of
study when looking at complex systems.
To illustrate an answer to the question of discovery, let me give you four pieces of
information: 1) Person X died of heart failure. 2) Person Y died of heart failure. 3) Death from
heart failure is a genetically inherited tendency. 4) Neither person X nor person Y needed to die
as early as they did if they had watched their diet and controlled their blood pressure.
Does this information carry any special meaning other than its face value? No, it is just
information about heart attacks. But now let me put the information into a context where it will
have a special meaning. Suppose you are told that person X is your father and person Y is your
grandfather. Suddenly you can connect all the information together into a meaningful pattern.
Since you now know there is a genetic connection, you have to worry about your odds of having
heart trouble. And since you know that something can be done to reduce the risk of heart attack,
you have to make some decisions about modifying your behavior. It is amazing how just a little
additional information suddenly pulls all the prior information together and casts it in a new light.
Sometimes it is just a little more information that is needed. Or sometimes it is just a different
perspective or a rearrangement of the existing information so that we see the relevant
connections.
It is fascinating that much of what is known, and sometimes what is believed to be new, is
simply wisdom that is very, very old. The Chinese believe in qi (also spelled ki, or chi), a term
that refers to 'vital energy'. Qi is a central theme in the most comprehensive early medical
document of China, the Huangdi Neijing, which dates from about 50 B.C. and summarizes the
medical knowledge at that time. The Chinese think of health as an issue of balance. The task of
the physician is to keep the various forces found inside the body in balance with the outside forces
acting on the body. The human body is thought of as the system that houses qi, which is the
essence of existence. No modern Western idea corresponds very closely to the range of meaning
of qi. Qi is a dual energy force of opposites that operates like polar forces in balance or in
harmony. Because qi permeates all living matter, some early thinkers held that matter was energy
in a stored or condensed form. Did you hear what I said? Some early Chinese wise men thought
that matter was energy. And then along comes Albert Einstein almost two thousand years later to
tell us that matter is energy! Did Einstein copy someone else's idea? No. We are back to the
question of boundaries. Where is the boundary of an idea? I am simply pointing out that the
body of knowledge that now exists has grown on what has gone before. There is a lot of useless,
bad, and inaccurate information floating around the world. But one has to think that basic ideas
that are able to persist for centuries must have some foundation of truth to them. It is for this
reason that I am not at all embarrassed to admit that some of the notions brought forth in the
Nomothetic Theorem echo ideas that have been passed down through the ages."
Opposing forces are one of these ideas. Polar forces, although struggling against each
other, can act in harmony.
For thousands of years the Chinese have interpreted the natural world in the context of
'yin' and 'yang'. To think in terms of yinyang, means to look at the universe as the product of two
interacting opposites. We often refer to yin and yang as forces. But perhaps force isn't the right
word. The opposites may be male and female, decaying and growing, tall and short. The
classification of a thing into yin or yang does not depend on its intrinsic nature as much as the role
it plays in relation to other things. Therefore man may be classified as yin in relation to heaven,
but as yang in relation to woman. Thus, the relative relationship of opposites is the salient trait
that defines yin and yang.
But the concept goes deeper than a simple comparison of opposites. When time is the
boundary between yin and yang, the focus is on the dynamics of the relationship. In other words,
the relationship between opposites is not a static one, but is thought to be a continuous cycle that
oscillates fluidly like a tug of war. Thus yang is day and yin is night. Yang is summer and yin is
winter. Like the ebb and flow of the tide, one folds into the other and then returns again. We
begin to see the idea of harmony in the form of flow, or gradual cycle of change.
Approximately two or three thousand years before the birth of Christ, a more complex
scheme of correlative thinking was developed based on a system of trigrams and hexagrams. A
trigram is an array of three horizontal lines, one above the other, some continuous and
representing yang, and some broken and representing yin. There are eight possible trigrams. The
origin of the original eight kua is believed to go back to emperor Fu Hsi (2852 - 2737 BC).
Legend holds that eventually this doctrine was recorded in the I-Ching, or 'Book of Changes', by
Wen Wang, one of the founders of the Chou dynasty (1122 - 249 BC), while he was in prison.
The author of the I-Ching used the eight trigrams in pairs, thus yielding sixty-four combinations.
To each of these sixty-four hexagrams some law of nature corresponds. The Chinese used the
Book of Changes as a manual of divination and believed that the combinations held all wisdom.
No hexagram is a static entity. Each combination is taken as representing a stage in a continuous
process of change.
The idea of cause and effect, which is common to Western thinking, is totally foreign to
traditional Chinese thought. Ponder for a moment the implications of a world governed solely by
cause and effect. If we knew all the causes and all the results, we could predict anything and
everything. At the beginning of the nineteenth century, a French scientist, the Marquis de
Laplace, proposed that the universe was completely deterministic. Laplace argued that there are
laws that govern everything that will happen. If we know the laws, then we shall know our fate.
In contrast to this, approximately 300 AD, Guo Xiang wrote, "What we call things, are all that
they are by themselves; they did not cause each other to become so." The Chinese believe that no
state of affairs is permanent, but also that change cannot be forced. There is a theme of harmony
interwoven with the cycle of change that comes from the duality of yin and yang. When the sun is
at its highest point, it is beginning to set. When the tide has fully retreated, it is beginning to
return. This natural cycle cannot or should not be tampered with by man. Therefore, you should
not be complacent when good fortune smiles on you; and you should not despair when you are
struck by misfortune. Nor can you cause or take credit for the way things are.
Laplace was wrong. Although there are laws that govern the universe, and the Theory of
Stability allows for prediction, Heisenberg's uncertainty principle and the Theory of Volatility
contradict determinism. Through the ages, the old beliefs have continued to stand the test of
time.
I confess to leaning toward the wisdom of the ancient philosophers. Long ago, they
declared that the basic elements of the universe were created by the interaction of two opposing
forces. When one force reached its limit, it became the other force. The universe was defined by
the unity of two polar forces. This polar energy, known as qi, is the basic substance of all
creation. I am hesitant to be too literally accepting. But the concept of balance, or harmony, is
essential to explain both stability and volatility.
Lao-tzu (604-517 BC) is another early philosopher. Although the dates of his life, and
even his very existence is in question, nevertheless his beliefs, or the wisdom derived from the
Tao-te-ching, is widely accepted. Taoism claims the universe is ever changing. Again, this harks
to the Theory of Volatility. Yet, while acknowledging change, Taoism seeks harmony with the
Tao, or path which the universe follows. It claims that everything is one: polarities are not in
opposition to one another but are only two aspects of a single reality. So we are presented with a
reality that is both ever changing and still united. There is a harmony between the stability of
unity and the volatility of change.
I hope you can see the similarity of these ancient philosophies with the duality of the
Nomothetic Theorem. Although at first it seems awkward to try to reconcile two opposing
concepts in the same theorem, there is actually harmony in the way they interrelate.
The Theory of Stability relies on the ability of forces to come into balance. This concept
of balance is dependent on symmetry. If a given force grows or diminishes in an unusual
sequence, if it oscillates, transitions, metamorphoses, or does anything either ordinary or unique,
its opposing force should display symmetrical qualities. If this isn't the case, then it is unlikely that
there can ever be any balance between forces, and any stability. Therefore, validation for the
Theory of Stability should come from finding symmetrical forces in nature. The inquisitive mind
of man has, through the science of physics over the last three hundred years, carefully investigated
and documented numerous different forces (or perhaps in some cases, different applications of the
same force) in the universe. It is now easy to look at our world in the light of this information and
see numerous examples of symmetry.
Simple magnetism is an excellent illustration of two polar forces. Every bar magnet has
two poles, a positive and a negative. If like forces are put together (a positive with a positive),
they repel. If opposite forces are placed together (a negative with a positive), they attract. The
unique thing about a magnet is that if you break it in half, each half still has a negative and a
positive pole at each end. You can subdivide a magnet as many times as possible and you will
never end up with a piece that just has one pole. The positive magnetic force cannot exist without
the opposite negative force! Isn't this a perfect example of yin and yang! Here is an example of
symmetry in opposites.
We now know that electricity and magnetism are related. The induction of one field force
by the other was not fully appreciated until the time of James Clerk Maxwell (1831-1879). But
one hundred years earlier Joseph Priestley (1733-1804) experimented with electromotive force,
the potential difference in electric charge. He found that if two oppositely charged bodies are
allowed to connect, directly or through a conductor, the charges neutralize each other.
Electricity, just like magnetism, carries a positive and negative charge. Once again, we see an
example of symmetry.
I have already mentioned Pascal's law (1647) which says that the force exerted on any
particle within an enclosed fluid is transmitted equally in all directions. This demonstrates stability
internally throughout the fluid. Where the fluid meets the wall of the container, the force of the
fluid, perpendicular to the wall at every point, is balanced by the opposing force of the wall. Thus
Pascal's law displays a balance of forces within a fluid and between a fluid and its container.
Archimedes (287-212 B.C.) understood symmetry (from which comes equivalence) when
he formulated his now famous principle of specific gravity. The buoyancy force acting on a
submerged body is equal to the weight of the fluid displaced. If the object floats, there is stability
from the balance between the gravitational force and the buoyancy force.
The Swiss mathematician Daniel Bernoulli (1700-1782) was looking for symmetry when
he sought to learn how pressure changes. Bernoulli's principle states that the total mechanical
energy of an incompressible and inviscid flow is constant along a streamline. The immediate
conclusion that can be drawn from this principle is that pressure decreases as velocity increases.
Once again, we are able to explain fluid and aerodynamic stability as a symmetry between two
forces: pressure and thrust, and their opposing forces: frictional drag and the gravitational force.
This is what makes airplanes fly. The shape of an airplane wing reduces pressure on its upper
surface creating lift. The lift increases as the velocity of the air passing over the wing increases.
When the force of lift (the relative difference in air pressure) is great enough to overcome and
then balance the force of gravity, the plane flies.
While Bernoulli's principle measures the relationship between pressure and velocity, many
years before, Robert Boyle (1627-1691) found a similar relationship between pressure and
volume. Boyle's law states that there is a direct inverse relationship between the external pressure
containing a gas and the volume of a gas at constant temperature. If the pressure is reduced by
one-third, the volume will triple. Boyle's law recognizes the symmetry between the force causing
a gas to expand versus the external pressure necessary to contain the gas.
In 1809, Joseph Louis Gay-Lussac found the same symmetry while studying the
relationship between volume and temperature. If a body of gas is held at a constant pressure, the
volume is directly proportional to the absolute temperature.
In 1787, Jacques Alexandre Cesar Charles compared pressure and temperature. If the
volume is held constant, pressure varies directly with temperature.
Am I boring you? The point is, there is a lot of symmetry between opposing forces in
nature (thankfully). Symmetry allows forces to come into balance and results in stability. If there
isn't some symmetry, some pattern repetition, some stability and durability which creates
dependability, we couldn't make accurate predictions.
I would like to take you through one more exercise that displays a symmetry of what
happens to forces over distance. I am going to show you some equations that describe different
physical phenomena. I don't care if you understand the math. All I want you to see is the
symmetry between the different equations that describe different forces in nature.
In 1777, Charles Augustin de Coulomb proposed Coulomb's law:
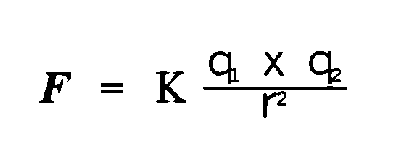 |
Coulomb's Law
The force between two electrically charged particles is proportional to the product of the charges
divided by the square of the distance that separates them.
In 1972, John Lennox Boyle proposed a second Boyle's law:
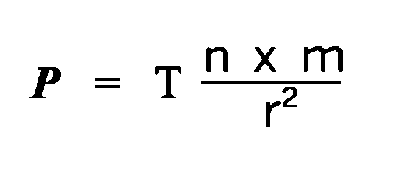 |
Boyle's Second Law
The expansive force of any volume of gas is proportional to the product of the temperature and
the total mass (number of molecules times the mass of each molecule) divided by the square of the
average distance that separates them.
In 1684, Sir Isaac Newton proposed Newton's law of gravity:
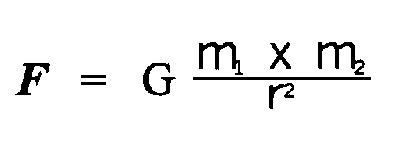 |
Newton's Law of Gravity
The gravitational force between two masses is proportional to the product of the masses divided
by the square of the distance that separates them.
It doesn't matter whether you understand these equations. You can see just by looking at
them that they all have the same form. In particular, the force varies inversely with the square of
the distance (r2) in all cases. This same relationship is found with sound, where
the intensity varies inversely to the square of the distance. The energy in all electromagnetic
waves also varies inversely to the square of the distance. This consistent relationship between
force and distance tells us about the consistent structure of our universe. As we witness
consistency in nature and more and more examples of symmetry between opposing forces, our
hopes are raised that forces can and do come into balance and there can be stability in the
universe.